Chapter 2

2. เสียง (Sound)


2.1 การเคลื่อนที่ของคลื่นเสียง

เสียงเป็นคลื่นกล เกิดจากการสั่นสะเทือนของแหล่งกำเนิดเสียง แล้วพลังงานผ่านอนุภาคของตัวกลาง เช่น อากาศ น้ำ และโลหะต่างๆ เป็นต้น 

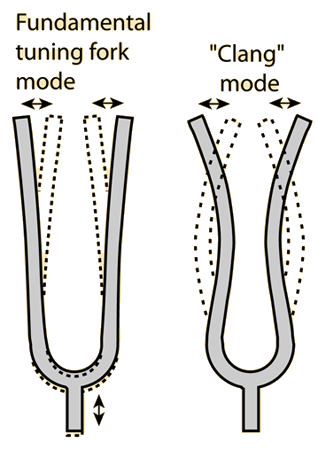
ภาพที่ ก. การสั่นของส้อมเสียง (Tuning Fork)

ดังภาพ เมื่อเคาะส้มเสียง ขาของส้อมเสียงจะสั่น ทำให้โมเลกุลที่อยู่รอบๆ ถูกบีบอัดขณะที่ขาของส้อมเสียงจะสั่น ทำใก้โมเลกุลของอากาศที่อยู่รอบๆ ถูกบีบอัดขณะที่ขาของส้อมเสียงกางออก และถูกขยายที่ขาของส้อมเสียงหุบข้าหากัน เกิดเป้นคลื่นแผ่ออกไป



เมื่อพิจารณาการเคลื่อนที่ของเสียงในอากาศ  ขณะที่เสียงผ่านอากาศโมเลกุลของอากาศจะเกิดการสั่นทำให้เกิดเป็นช่วงอัด (compression) และช่วงขยาย (rarefaction)




 ขณะที่คลื่นเสียงเคลื่อนที่ผ่านตัวกลางทำให้อนุภาคของตัวกลางเคลื่อนที่เกิดการอัด (Compressions) และการขยาย (Rarefaction) ที่เปลี่ยนไปจากสภาวะปกติ 

อ้างอิงจาก
  1. http://www.sa.ac.th/winyoo/Sound/Applets/Waves/Lwave01/Lwave01Applet.html
  2. หนังสือเรียนวิชาพื้นฐาน วิทยาศาสตร์ "พลังงาน"


2.2 อัตราเร็วของคลื่นเสียง
อัตราเร็วของเสียง คือ ระยะทางที่เสียงเดินทางไปในตัวกลางใดๆ ได้ในหนึ่งหน่วยเวลา โดยทั่วไปเสียงเดินทางในอากาศที่มีอุณหภูมิ 25°C (= 298,15 K) ได้ประมาณ 346 เมตร/วินาที และในอากาศที่อุณหภูมิ 20°C ได้ประมาณ 343 เมตร/วินาที อัตราเร็วที่เสียงเดินทางได้นั้นอาจมีค่ามากขึ้นหรือน้อยลงขึ้นอยู่กับอุณหภูมิของตัวกลางเป็นหลักและอาจได้รับอิทธิพลจากความชื้นบ้างเล็กน้อย แต่ไม่ขึ้นกับความดันอากาศ

เนื่องจากการเดินทางของเสียงอาศัยการสั่นของโมเลกุลของตัวกลาง ดังนั้นเสียงจะเดินทางได้เร็วขึ้นหากตัวกลางมีความหนาแน่นมาก ทำให้เสียงเดินทางได้เร็วในของแข็ง แต่เดินทางไม่ได้ในอวกาศ เพราะอวกาศเป็นสุญญากาศจึงไม่มีโมเลกุลของตัวกลางอยู่

การคำนวณอัตราเร็วเสียง
อัตราเร็วของเสียง c โดยทั่วไปคำนวณหาได้จาก
c = \sqrt{\frac{C}{\rho}}
โดย
C คือ สัมประสิทธิ์ของความแข็งเกร็ง (coefficient of stiffness)
\rho คือ ความหนาแน่น
ดังนั้น อัตราเร็วของเสียง จะเพิ่มขึ้นตามความแข็งเกร็งของวัสดุ และ ลดลงเมื่อความหนาแน่นเพิ่มขึ้น
อัตราเร็วของเสียงในของแข็ง
ของแข็งนั้นมีค่าความแข็งเกร็งไม่เป็นศูนย์ ทั้งต่อแรงบีบอัด หรือ การเปลี่ยนปริมาตร (volumetric deformation) และ แรงเฉือน (shear deformation) ดังนั้นจึงเป็นไปได้ที่จะกำเนิดคลื่นเสียงที่มีความเร็วต่างกัน ขึ้นกับรูปแบบของคลื่น
ในแท่งของแข็ง ซึ่งมีขนาดความหนา (หรือขนาดของตัวกลาง ในแนวตั้งฉากกับการเคลื่อนที่ของคลื่น) เล็กกว่าความยาวคลื่นมาก อัตราเร็วของเสียงหาได้จาก
c_{\mathrm{solid (thin), longitudinal}}= \sqrt{\frac{E}{\rho}}
โดย
E คือ มอดุลัสของยัง
\rho (rho) คือ ความหนาแน่น
ดังนั้น ในเหล็ก อัตราเร็วของเสียงจะมีค่าประมาณ 5100 m/s
ในแท่งของแข็งหนา หรือ ขนาดด้านข้างของตัวกลาง ใหญ่กว่าความยาวคลื่น เสียงจะเดินทางได้เร็วกว่า อัตราเร็วของเสียงสามารถหาได้จากการแทนค่ามอดุลัสของยัง ด้วย มอดุลัสคลื่นหน้าราบ (en:plane wave modulus) ซึ่งหาได้จาก มอดุลัสของยัง และ อัตราส่วนของปัวซง (en:Poisson's ratio) \nu
M = E \frac{1-\nu}{1-\nu-2\nu^2}
ดังนั้น อัตราเร็วของเสียง
c_{\mathrm{solid (thick), longitudinal}} = \sqrt{E \, ( 1- \nu) \over \rho \, ( 1- \nu - 2 \nu^2) } .

สำหรับคลื่นตามขวางนั้น มอดุลัสของยัง E จะถูกแทนด้วย ค่ามอดุลัสของแรงเฉือน (en:Shear modulus) G
c_{\mathrm{solid, transverse}} = \sqrt{G \over \rho} .
จะเห็นได้ว่า อัตราเร็วของเสียงในของแข็งขึ้นกับความหนาแน่น ของตัวกลางเท่านั้น โดยไม่ขึ้นกับอุณหภูมิ ของแข็งเช่น เหล็ก สามารถนำคลื่นด้วยความเร็วที่สูงกว่าอากาศมาก

อัตราเร็วของเสียงในของเหลว

ของเหลวจะมีความแข็งเกร็งต่อแรงอัดเท่านั้น โดยไม่มีความแข็งเกร็งต่อแรงเฉือน ดังนั้นอัตราเร็วของเสียงในของเหลวหาได้โดย
c_{\mathrm{fluid}} = \sqrt {\frac{K}{\rho}}
โดย
K คือ มอดุลัสของการอัดแอเดียแบติก (adiabatic en:bulk modulus)

อัตราเร็วของเสียงในก๊าซ

ในก๊าซ ค่า K สามารถประมาณโดย
K=\kappa \cdot p
โดย
κ คือ ดัชนีแอเดียแบติก (en:adiabatic index) บางครั้งใช้สัญลักษณ์ γ
p คือ ความดัน
ดังนั้น อัตราเร็วของเสียงในก๊าซสามารถคำนวณได้โดย
c_{\mathrm{gas}} = \sqrt {{\kappa \cdot p}\over\rho}
ในกรณี ก๊าซในอุดมคติ (en:ideal gas) จะได้
c_{\mathrm{ideal\,gas}} = \sqrt {\kappa \cdot R\cdot T}  โดย
  • R (287.05 J/(kg·K) สำหรับอากาศ) คือ ค่าคงที่ของก๊าซ (en:gas constant) สำหรับอากาศ: ปกติในทางอากาศพลศาสตร์ ค่านี้หาจาก การหารค่าคงที่ของก๊าซสากล R(J/(mol·K)) ด้วย ค่ามวลโมล (en:molar mass) ของอากาศ
  • κ (kappa) คือ ค่า ดัชนีแอเดียแบติก (en:adiabatic index) (เท่ากับ 1.402 สำหรับอากาศ) บางครั้งเขียนแทนด้วยสัญลักษณ์ γ
  • T คือ ค่าอุณหภูมิสัมบูรณ์ (เคลวิน)
(นัวตัน นั้นค้นพบวิธีการหาค่าอัตราเร็วของเสียงก่อนพัฒนาการของ อุณหพลศาสตร์ และได้ใช้การคำนวณแบบอุณหภูมิเสมอ (en:isothermal) แทนที่จะเป็นแบบแอเดียแบติก(en:adiabatic) ซึ่งทำสูตรของนิตันนั้นขาดตัวคูณ κ)

ไม่มีความคิดเห็น:

แสดงความคิดเห็น

สมัครสมาชิก: บทความ (Atom)